vovaemerald.blogg.se - Hanoi towers recursive function

Hanoi towers recursive function code#
Hanoi towers recursive function license#

These disks are continuously moved by priests in the temple. There is a story about an ancient temple in India (Some say it’s in Vietnam – hence the name Hanoi) has a large room with three towers surrounded by 64 golden disks.

Hanoi towers recursive function license#

"Programming via Java" by By Carl Burch, used under Creative Commons Attribution-Share Alike 3.0 License license.ĬC BY-SA 4.0 Creative Commons Attribution-ShareAlike 3.0 Unported LicenseĬreative Commons Attribution 4.Tower of Hanoi game is a puzzle invented by French mathematician Édouard Lucas in 1883.

"Recursion (computer science)", Wikipedia under Creative Commons Attribution-ShareAlike 3.0 Unported License.Ĭode example, explanation and diagram for Fibonacci Recursion in Java & "Anagrams" from

Hanoi towers recursive function code#

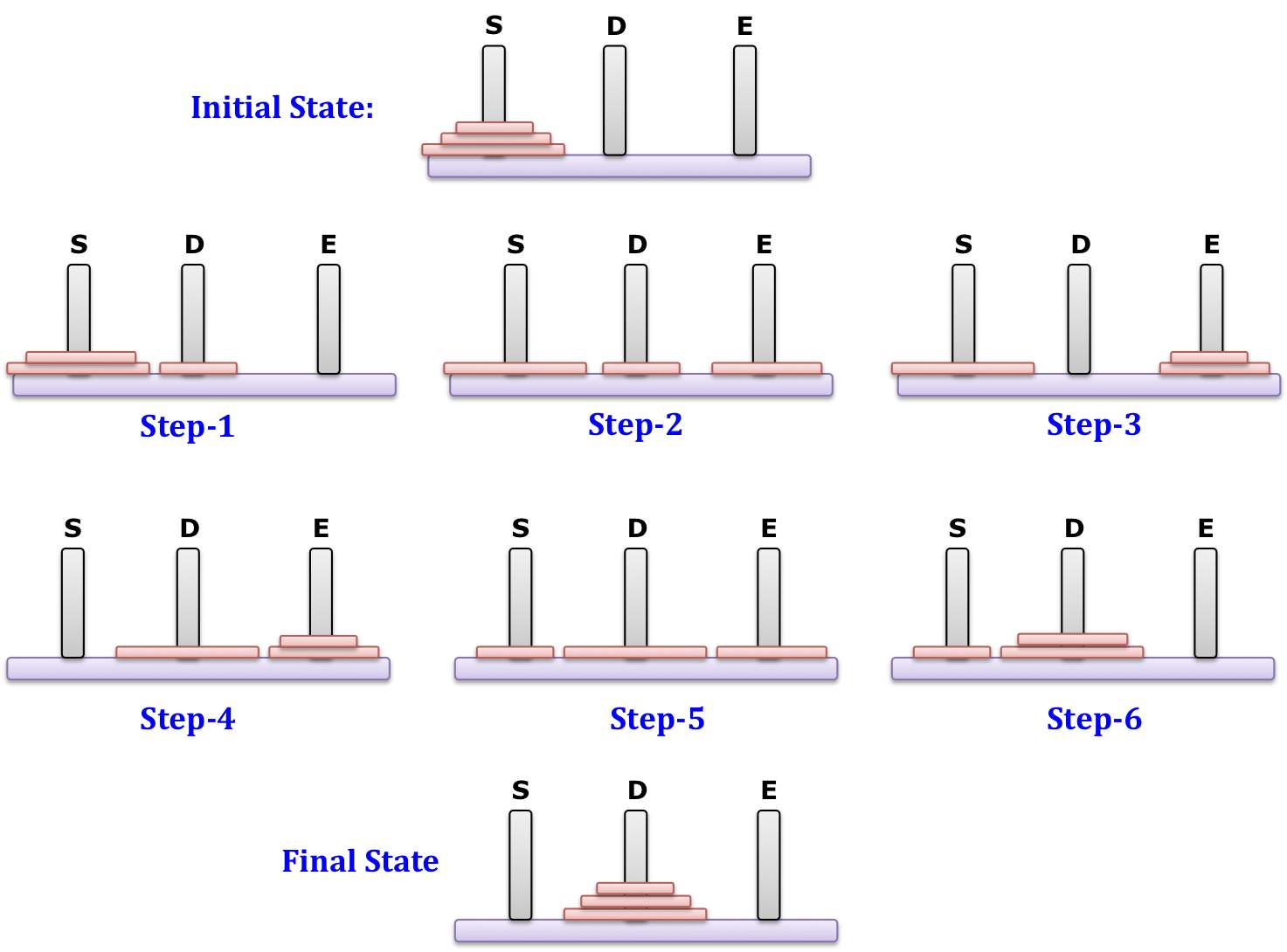
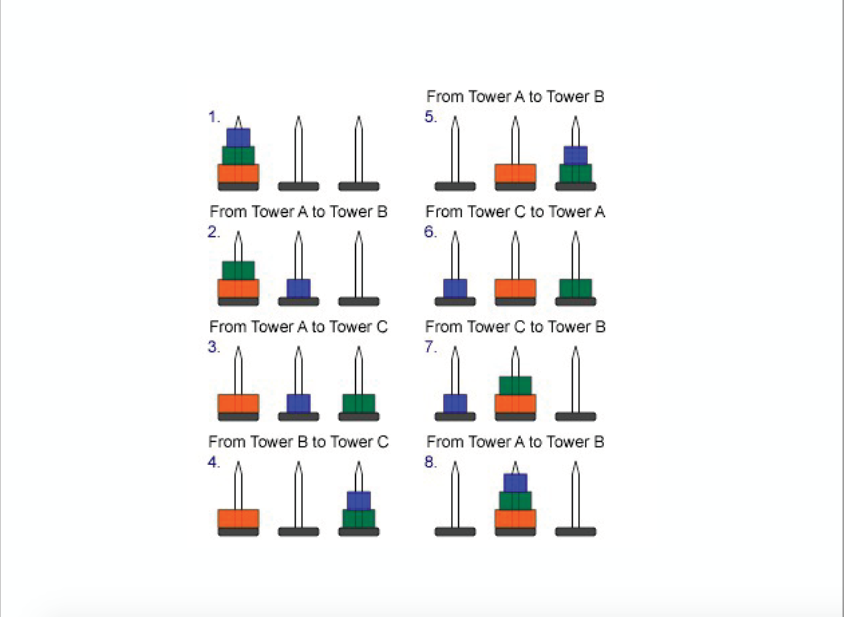
Chris Bourke used under Creative Commons Attribution 4.0 International license. This work is available under a Creative Commons Attribution 4.0 International License.Ĭhapter on Memoization is a derivative of "Algorithms" by Jeff Erickson used under Creative Commons Attribution 4.0 International license. This book is licensed under Creative Commons Attribution- ShareAlike 4.0 International License Original Content CC-BY-SA 4.0 Internationalīy Prof. We will return to this when we discuss recurrence relations a bit later.Ĭopyright (C) CodeAhoy. If we were to measure the steps by how many times a disk is moved from one peg to another, then the interesting question is how many moves this makes when given an initial set of N disks on a peg. What is not clear is how many steps this takes. Alternatively, we could just store this sequence in an array of strings that could be passed back via a parameter and then printed by the calling code. The function produces, as its output, a sequence of statements showing which disk was moved. The recursion stops when the problem size is 1. In each call the problem size is smaller. This is an example of a recursive algorithm with three recursive calls. Typedef char peg void towers ( int count, peg source, peg dest, peg spare ) Now all disks will be on peg B in the correct order.

Solve the problem for moving n − 1 disks from peg C to peg B.

Move the bottom disk from peg A to peg B.

Ignore the bottom disk and solve the problem for n − 1 disks, moving them to peg C instead of peg B.

This is a problem with no obvious, simple, non-recursive solution, but it does have a very simple recursive solution:

A larger disk may never be on top of a smaller disk.

Only the top disk can be moved from its stack and.

The problem is to devise an algorithm that will move all of the disks to peg B moving one disk at a time subject to the following two rules: The largest is therefore at the bottom of the pile and the smallest at the top. Way that above any disk are only smaller disks. Initially, n disks of different sizes are arranged on peg A in such a You are given three pegs, labeled A, B, and C. Of the other needles, tower, temple, and Brahmins alike will crumble into dust,Īnd with a thunderclap the world will vanish. When the sixty-four discs shall have been thus transferred from the needle on which at the creation God placed them to one Than one disc at a time and that he must place this disc on a needle so that Laws of Bramah, which require that the priest on duty must not move more Day and night unceasingly the priests transfer the discs from one diamond needle to another according to the fixed and immutable On one of these needles, at theĬreation, God placed sixty-four discs of pure gold, the largest disc resting on the brass plate, and the others getting smaller and smaller up to the top one. The world, rests a brass plate in which are fixed three diamond needles, eachĪ cubit high and as thick as the body of a bee. beneath the dome which marks the centre of The following year, Henri de Parville described the puzzle with the following Claus (de Siam)” (an anagram of “Lucas d’Amiens”) as an actual physical puzzle. The Tower of Hanoi puzzle was first published by the French teacher and recreational mathematician Édouard Lucas in 1883, under the pseudonym “N.